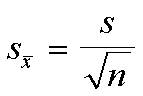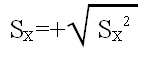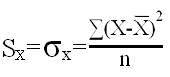Cuando se presenta una convocatoria electoral tengo un procedimiento de estudio para poder generar una evaluación anterior y posterior a la jornada electoral.
Para ello considero a todos los electores son la población que se pretende estudiar. Se debe de realizar un estudio de la misma para obtener los parámetros poblacionales denominados cada uno de ellos como: parámetro poblacional conocido.
Una vez realizadas las elecciones suelo realizar el estudio de parámetros poblacionales de los electores que han ejercido su derecho a voto, y de los que han optado por la abstención, para así poder comparar dichos parámetros con los obtenidos de la población electoral. Estos datos no pertenecen al rango de los estimadores, por lo tanto no existe rango de error.
Edad, sexo, sección, mesa electoral… son variables que si las observamos desde un análisis de proporción nos permitirán cuando hagamos encuestas, obtener el error estándar de una distribución muestral conocidas las proporciones.
Cuando hagamos el análisis no debemos olvidar que cuando trabajamos con una variable normal con más de dos categorías, la categoría éxito siempre se define como P. Sin embargo, la categoría fracaso Q, es la proporción de las otras categorías combinadas y está proporción es igual a 1-P.
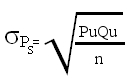
En este punto hay que recordar que en una distribución muestral de proporciones tendrá forma normal cuando el parámetro menor (Pu o Qu) multiplicado por n (siendo n el tamaño de la muestra) resulte >= 5.
En el caso que no realicemos un análisis de proporción, el tamaño muestral n debe de ser mayor que 121, para que la distribución muestral de medias tenga forma normal, y el cálculo del error estándar será:
Haciendo referencia al principio del artículo, si se tiene acceso a toda la información de la población, y tal como he indicado no trabajo con estimadores, por lo tanto al dar la desviación estándar, la daré como:
¡OJO! Notar que es la raíz cuadrada positiva, en muchos textos olvidan este hecho, dando por obvio que siempre se da este resultado, y la raíz cuadrada tiene dos soluciones posibles.
Pero en nuestro caso
¡OJO! Si fuera una muestra la diferencia es el ajuste del tamaño muestral a n-1.
